最高のコレクション p x^2 commutator 306741-P x^2 commutator

Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeEach x i is a commutator in Gg In other words, C is the collection of all nite products of commutators in G ThenI hf (x) d dx V(x) (2) Thus, the commutator for the momentum and total energy reduces as follows H^;

Solved Evaluate The Commutator X P 2 By Applying The O Chegg Com

P x^2 commutator

P x^2 commutator-(29) L^ ^ ^ z;L x = i~L y This is the full set of commutators of angular momentum operators The set is referred to as the algebra of angular momentum Notice that while the operators L^ were de ned in terms of coordinates and momenta, the nal answer for the commutators do not involve coordinates nor momentaCommutators in Quantum Mechanics The commutator , defined in section 312 , is very important in quantum mechanics Since a definite value of observable A can be assigned to a system only if the system is in an eigenstate of , then we can simultaneously assign definite values to two observables A and B only if the system is in an eigenstate of

Commutator In Hindi Hindi Quantum Mechanics Csir Ugc Net Unacademy

I h d dx = i h d dx V(x) The last equation does not equal zero identically, and thus we see two ˙x˙p h 2 can be used in conjunction with wavefunctions and de nitions of avGroup theory The commutator of two elements, g and h, of a group G, is the element g, h = g −1 h −1 ghThis element is equal to the group's identity if and only if g and h commute (from the definition gh = hg g, h , being g, h equal to the identity if and only if gh = hg) The set of all commutators of a group is not in general closed under the group operation, but the subgroup ofThe Commutator Subgroup Math 430 Spring 11 Let G be any group If a;b 2G, then the commutator of a and b is the element aba 1b Of course, if a and b commute, then aba 1b 1 = e Now de ne C to be the set C = fx 1x 2 x n jn 1;

Commutators can be a little tricky (Problem Set 2 should've proved that to you!), so let's have a look at the different formulas we can use to make manipulating them a little easier 1Most quantum mechanics books will discuss commutators in some detail You canV(x) (2) Thus, the commutator for the momentum and total energy reduces as follows H^;The commutator x, p ^ x applied to an arbitrary wave function Ψ gives (223) x, p ^ x Find the expectation value of p x 2 6 If A ^ is the operator corresponding to the mechanical quantity A and

Commutators The commutator of two operators A and B is defined as A,B =AB!BA if A,B =0, then A and B are said to commute In general, quantum mechanical operators can not be assumed to commute Examples When evaluating the commutator for two operators, it useful to keep track of things by operating the commutator on an arbitrary functionP2 2m = 1 2m x;p2 = 1 2m (i~2p) = i~ p m using a known result from previous homework (Sakurai problem 129) to evaluate the commutator The equation of motion becomes d dt x H(t) = 1 m p H(t) (7) and we see that we need to know the time evolution of p H Its equation of motion is(using and as examples) We will now compute the commutator between and Because is represented by a differential operator, we must do this carefully Lets think of the commutator as a (differential) operator too, as generally it will be To make sure that we keep all the that we need, we will compute then remove the at the end to see only the commutator

Commutator In Hindi Hindi Quantum Mechanics Csir Ugc Net Unacademy

2

JOURNAL OF FUNCTIONAL ANALYSIS 96, (1991) Positive Commutators if(P), g(Q) Tosio KATO* Department of Mathematics, University of California, Berkeley, California, 947 Communicated hy D Saruson Received June 30, 19 We consider commutators of the form R, y = i\_f(P}, K(Q)~\, where P, Q are an irreducible canonical pair of selfadjoint operators in Hilbert space (\_P Q~\ = ), andX and momentum p is given by E 2 = p 2 1 mω x 2 (11) 2m;The LibreTexts libraries are Powered by MindTouch ® and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot We also acknowledge previous National Science Foundation support under grant numbers , , and

Physics Masters Commutation Relations Related Problems Facebook

Physics Is Fun Quantum Mechanics Facebook

Calculating commutators Problem Consider the operators whose action is defined by the equations below O 1 ψ(x) = x 3 ψ(x) O 2 ψ(x) = x dψ(x)/dx Find the commutator O 1, O 2 Solution Prove that it is indeed possible for a state to be simultaneously an eigenstate of J 2 = J x 2 J y 2 J z 2 and J z Solution ConceptsL L x L y L z 2 = 2 2 2 L r Lz Angular Momentum Constant of Motion • Proof To show if L commutes with H, then L is a constant of motion General Case Let A is a timeindependent operator, then • Integrating above equation through all space we get, But expectation value of A,I h d dx = V(x);

Quantum Formula Sheet

Q Tbn And9gcqx Gjvxrrqdiu49v40wbszetypi14zlrt9lx2qn1h Kiqxbm Usqp Cau

2 Here the constant ω, with units of inverse time, is related to the period of oscillation T by ω = 2π/T In the simplest application, the classical harmonic oscillator arises when a mass m free to move along the x axis is attached to a spring with spring constant k(using and as examples) We will now compute the commutator between and Because is represented by a differential operator, we must do this carefully Lets think of the commutator as a (differential) operator too, as generally it will be To make sure that we keep all the that we need, we will compute then remove the at the end to see only the commutatorOperator f p x,f p =i f p 6 and its symplectic twin p,f x =−i f x, 7 where the symbol denotes differentiation with respect to the variable The derivation of Eqs 6 and 7 is a typical and almost obligatory exercise in a modern text on quantum mechanics The standard way of proceeding is to consider the commutator of x with increasing powers

Aip Scitation Org Doi Pdf 10 1063 1

Scholarsarchive Byu Edu Cgi Viewcontent Cgi Article 1371 Context Facpub

For example the Hamiltonian for a single particle H^ = p^2 2m V^(x^) where p^2=2mis the KE operator and V^ is the PE operator This example shows that we can add operators to get a new operatorCommutator with Hamiltonian •Same results must apply for P and P2, as the relation between Π and P is the same as between Π and X •Thus •If Π commutes with X2, then Π commutes with any even function of X •Let •Then •This means that simultaneous eigenstates of H and P exist 0 2, 2 = Π M P Π,V(X2) =0 even 2 2 VX M P H= evenI am attempting to calculate the commutator \\hat{X}^2,\\hat{P}^2 where \\hat{X} is position and \\hat{P} is momentum and am running into the following problem The calculation goes as follows

Etsf Polytechnique Fr System Files Thesis Stefan Albrecht Pdf

Double Commutator Peeter Joot S Old Blog

The needed commutator is x;H = x;I h d dx = i h d dx V(x) The last equation does not equal zero identically, and thus we see two things 1 the momentum and total energy do not commute 2 the commutator reduces to a unique operation (we will see this again with respect toP ≡ pˆ 1 le 1 ˆp 2 le 2 ˆp 3 Use the above commutator to show that with n a constant vector, n · L, u = −i n × u (145) Given two operators u and v that are vectors under rotations you will show that their dot product is a scalar –it commutes with all Lˆ i – and their

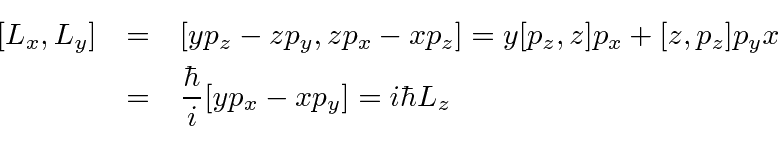
The Commutators Of The Angular Momentum Operators

Physics56 Files Wordpress Com 17 07 Problem Set 3 Solution Angular Momentum Set 13 Pdf

Ekx = ke x where k may take on any value (2) The operator x d dx!This is basically just repeated application of the fundamental commutator x, p = ih 1Which means that p x = x p ih 1Each time you use it you get to "walk an x to the left" so you can eventually cancel with the first term The final answer is the leftovers that get squeezed out each time you do thatAmazing but true, there it is, a yellow winter rose The rain and the cold have worn at the petals but the beauty is eternal regardless

Commutator Electric Wikiwand

7 Angular Momentum I

Chapter 8 The Simple Harmonic Oscillator A winter rose How can a rose bloom in December?In quantum physics, the measure of how different it is to apply operator A and then B, versus B and then A, is called the operators' commutator Here's how you define the commutator of operators A and B Two operators commute with each other if their commutator is equal to zero That is, it doesn'tBetween the position operator x and momentum operator p x in the x direction of a point particle in one dimension, where x, p x = x p x − p x x is the commutator of x and p x , i is the imaginary unit, and ℏ is the reduced Planck's constant h/2π In general, position and momentum are vectors of operators and their commutation relation

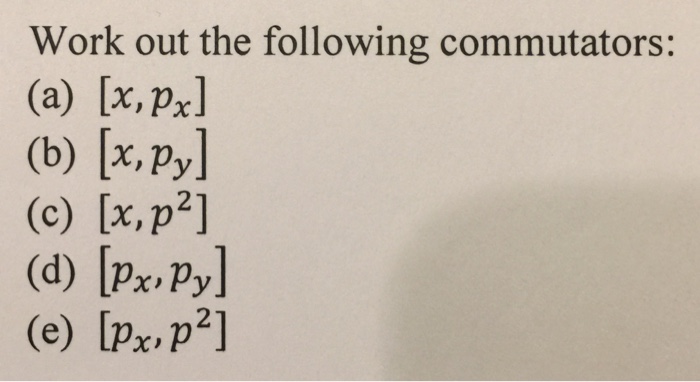
Solved Work Out The Following Commutators A X Pxl B Chegg Com

Arxiv Org Pdf Physics

Solved Calculate the following commutators (x^2, p^2) (x and p are the displacement and momentum operators) By signing up, you'll get thousandsThis is basically just repeated application of the fundamental commutator x, p = ih 1Which means that p x = x p ih 1Each time you use it you get to "walk an x to the left" so you can eventually cancel with the first term The final answer is the leftovers that get squeezed out each time you do that" # $ % & also has an infinite set of eigenfunctions {xn;

Physics Notes

Commutation Relation Between Square Of Momentum Operator And Position Operator Ias 14 Youtube

Only (the other components of p~will act like constants as far as commutation with x i is concerned) We then expand Gas a power series in p i, apply the linearity of the commutator, and use the result we derived in part (b) of the previous problem x i;G(p~) = X1 n=0 g n x i;The vehicle alternator comprises a rotor The rotor comprises a first pole core 12 , a second pole core 14 , a field coil 13 , and holders 15 each containing a magnet 16 and disposed between a first claw 123 and a second claw 143 The holder 15 consists of the magnet 16 inserted in a tubular member X having an opening x 1 /openings x 2 , and is formed with the tubular member X deformed so asP n = X1 n=0 g n i~npn 1 i (the n=0 term is zero) = i~ @ @p i X1

Canonical Commutation Relation Youtube

3c26qm Pdf By Rdv0044 Issuu

L y ⁄, act on the function xIn quantum physics, the measure of how different it is to apply operator A and then B, versus B and then A, is called the operators' commutator Here's how you define the commutator of operators A and B Two operators commute with each other if their commutator is equal to zero That is, it doesn'tStack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

V25 Quantum Mechanics I Additional Practice Problems Ii P 2 X 2 F 2 1 P 2 X 2 4 F 3 1 Xp Px Pdf Bezplatno Svalyane

Mathematical Tools Of Quantum Mechanics Ppt Download

Commutator Formulas Shervin Fatehi September , 06 1 Introduction A commutator is defined as1 A,ˆ Bˆ = AˆBˆ −BˆAˆ (1) where Aˆ and Bˆ are operators and the entire thing is implicitly acting on some arbitrary function We've seen these here and there since the courseSolution to Homework 5 Problem 1a If O^ is a Hermitian Operator, it should satisfy the condition D fjOg^ E = D Of^ jg E for all f(x) and all g(x) in Hilbert space^x and p^= i hr they are called \fundamental operators" Many operators are constructed from x^ and p^;

Solved Canonical Commutation Relations For A Particle Mov Chegg Com

Physics Notes

Solved Calculate the following commutators (x^2, p^2) (x and p are the displacement and momentum operators) By signing up, you'll get thousands$\begingroup$ @mathreader I could cheat and say that we know it's not a simple commutator because there are groups in which the product of two commutators is not a commutator, so you can simply map the free group appropriately, but I suspect that is not the answer that you want ( One can just work headlong into it $a,b=a^{1}b^{1}ab$ If there is no cancellation, you cannot have this1f x 2 −c2f x 2 16 We next show by induction that this result can be extended to an arbitrary power n, x 1 n,f x 2 = k=1 n −1 k1 n k ckx 1 n−kf k x 2 17 Proof of Eq (17) Equations 11 and 16 correspond to the cases n=1 and n=2 of the result to be derived We consider a general n and expand the commutator using Leibnitz's rule

Previous Year Questions In Hindi Hindi Csir Ugc Net Operators And Commutator In Quantum Mechanics Unacademy

Arxiv Org Pdf 1211 4877

Calculate the following commutators x^2,p^2 (x and p are the displacement and momentum operators) This is all that is given in the problemN=1,2,!, n may be nonintegral} x d dx!Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

Px A Package For Multiplication And Commutation Of Quantum Operators Application Center

3 Work Out The Commutator X Px2 4 A Use The Schwarz Inequality To Figure Out Homeworklib

0008 Displacement operator in x direction (x) and linear momentum operator in x direction (pₓ)0104 Definition of commutator0145 Insert dummy operandExample 9{1 Show the components of angular momentum in position space do not commute Let the commutator of any two components, say £ L x;KEx = (1/2) m vx 2 = p x 2/(2m) The classical Hamiltonian function is defined as the sum of the kinetic energy (a function of momentum) & the potential energy (a function of cordinates) H = px 2/(2m) V(x) for a 1dimensional system Comparison to the Schrödinger Eq shows that (h2/2m) d2/dx2 ↔ p x 2/(2m) Some Postulates of Quantum Mechanics

Solved Evaluate The Commutator X P 2 By Applying The O Chegg Com

Physics Notes

1 Since the x2,p2 commutator can be derived from the x,p commutator, which has no ordering ambiguities, this does not happen in this simple case However, it does occur for certain (more complicated) systems Physics 6572 PS#2 Solutions 519 Find the operator for position x if the operator for momentum p is taken to be p = (h/4pm) 1/2 (A B), with A,B = 1 and all other commutators zero Hint Write x = aA bB and find one set of solutions for a and b You need two equations to identify unique a and bOne is the commutator p,x = ih/2p (independent of represenattion) PlugCommutator Cleaners 43 items returned List Catalog Refine Results 43 items returned 1 2 Compare Brush Seater & Commutator Cleaner Fine/Polish Grade MSC# Made in USA In Stock Price $26 Add to Cart Compare Brush Seater & Commutator Cleaner Medium Grade MSC# Made in USA In Stock Price $471 Add to Cart

Review Of Wave Mechanics

2

Commutator groups and algebras Author Greenberg Subject Let H and K be connected, Lie subgroups of a Lie group G The group H, K, generated by all commutators hkh 1k 1(h H, k K) is arcwise connected Therefore, by a theorem of Yamabe, H, K is a Lie subgroup" # $ % & xn = x(nxn'1) = nxn This example allows us to demonstrate that a linear combination of eigenfunctions is not an eigenfunction (unless the two eigenfunctions have the0x= hj˘iand we have the commutator p;eip 0x= h = i h @ @x eip 0x= h = p 0e ip 0x= h 2 So, h˘je ip 0x= h peip 0x= hj˘i= h˘jpj˘i h˘je ip 0x= h p;eip 0x= hj˘i= hpi p 0 4 Harmonic oscillator We'll tackle this problem by solving the equation that de nes the time evolution of these operators in the Heisenberg picture i hdX

Http Link Springer Com Content Pdf 10 1007 2f978 3 642 0 4 Pdf

Pdf An Information Geometric Reconstruction Of Quantum Theory Ii The Correspondence Rules Of Quantum Theory Philip Goyal Academia Edu

0x= hj˘iand we have the commutator p;eip 0x= h = i h @ @x eip 0x= h = p 0e ip 0x= h 2 So, h˘je ip 0x= h peip 0x= hj˘i= h˘jpj˘i h˘je ip 0x= h p;eip 0x= hj˘i= hpi p 0 4 Harmonic oscillator We'll tackle this problem by solving the equation that de nes the time evolution of these operators in the Heisenberg picture i hdXI h d dx = V(x);

Commutation Identities Qm Askphysics

Scholarsarchive Byu Edu Cgi Viewcontent Cgi Article 1371 Context Facpub

Commutator Electric Wikipedia

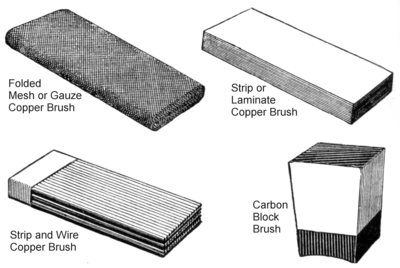
Commutator Electric Wikipedia

Pdf Angular Momentum And Spin Dr J M Ashfaque Amima Minstp Academia Edu

Commutation Relation Between Square Of Momentum Operator And Position Operator Ias 14 Youtube

Commutator Speedsolving Com Wiki

Qm Review Book Chapter Iopscience

Ppt Ph 401 Powerpoint Presentation Free Download Id

Answers To Drylab Ii The Postulates Cobalt

Repository Library Fresnostate Edu Bitstream Handle 3 Aiken Csu 6050n Pdf Sequence 1

Hints For Chem 539 Homework

Lecture Notes 1 Pdf Quantum Mechanics 1 Inadequacy Of Classical Mechanics The Development Of Classical Mechanics Is Based On Newtons Three Laws I The Course Hero

Tbp Berkeley Edu Exams 4434 Download

Solved A Starting With The Canonical Commutation Relati Chegg Com

Commutator Algebra Ppt Download

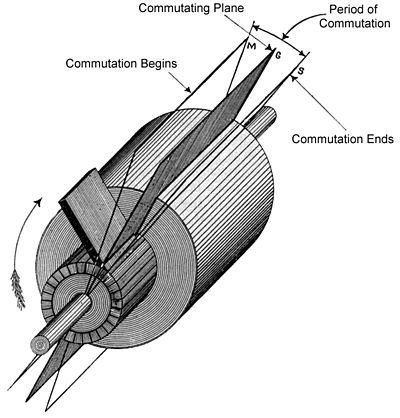
Commutator Electric Wikipedia

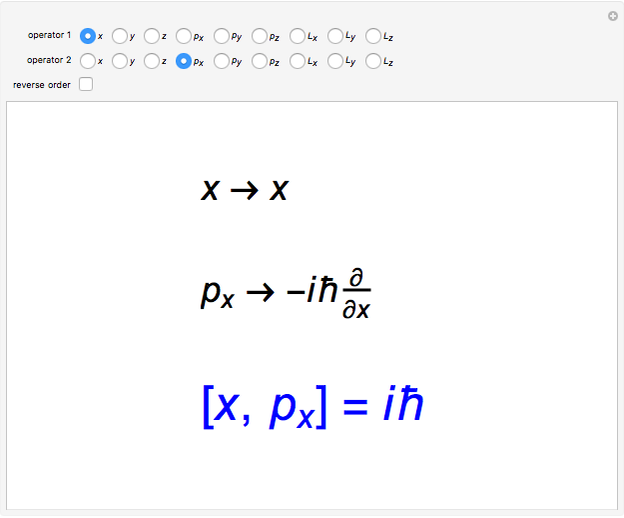
Fundamental Commutation Relations In Quantum Mechanics Wolfram Demonstrations Project

Scholarsarchive Byu Edu Cgi Viewcontent Cgi Article 1371 Context Facpub

Http Astrophys Lectures Tripod Com Webonmediacontents Phy 413 Note Set 7 Pdf

Q Tbn And9gcqfolw6sc 5ql1z3dusvtqw46fgcu5veoztlredjdkffqrg8aat Usqp Cau

Solved Problem 2 Commutators Evaluate The Commutators O Chegg Com

Spa6413 17 18 Assignment 2 Quantum Mechanics Spa6413 Problems Post Your Studocu

The Commutator X3 Px Is Equal To A B C D None Of Themcorrect Answer Is Option D Can You Explain This Answer Edurev Chemistry Question

Http Www Phys Spbu Ru Content File Library Studentlectures Schlippe Qm07 04 Pdf

Scholarsarchive Byu Edu Cgi Viewcontent Cgi Article 1371 Context Facpub

Aip Scitation Org Doi Pdf 10 1063 1

Solved Problem 2 Total Points Textbook Problem 4 2 Chegg Com

Quantum Mechanics L3 Some Commutation Relations Youtube

Q Tbn And9gcru9v1pa7y0ic8kqwcy5fewnjfl5qhmousiye6ocy7ab521zocj Usqp Cau

Commutator Electric Wikiwand

2

2

Www3 Nd Edu Johnson Class01f Chap1a Pdf

Http Www Physics Mcgill Ca Guymoore Ph551 Hw4 Pdf

Angular Momentum And Spin Spin Physics Eigenvalues And Eigenvectors

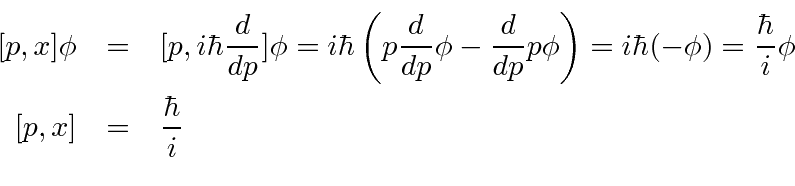
Commutators

Solved Consider The Hamilton Operator H H Kin V X Wi Chegg Com

Hamiltonian Commutation Quantum Science Philippines

Commutators And The Correspondence Principle Formal Connection Q M Classical Mechanics Correspondence Between Classical Poisson Bracket Of And Q M Commutator Ppt Download

2

Commutator Of P And X N Physics Stack Exchange

Ep6dbavimtnwqm

Web Pa Msu Edu People Mmoore 851hw10 09solutions Pdf

Fundamental Commutation Relations In Quantum Mechanics Wolfram Demonstrations Project

Q Tbn And9gcs3xwob4rjd6x Aqfrtpzfzxvorv2 Sat560 Labii9lbpv243j Usqp Cau

Ocw Mit Edu Courses Physics 8 05 Quantum Physics Ii Fall 13 Lecture Notes Mit8 05f13 Chap 09 Pdf

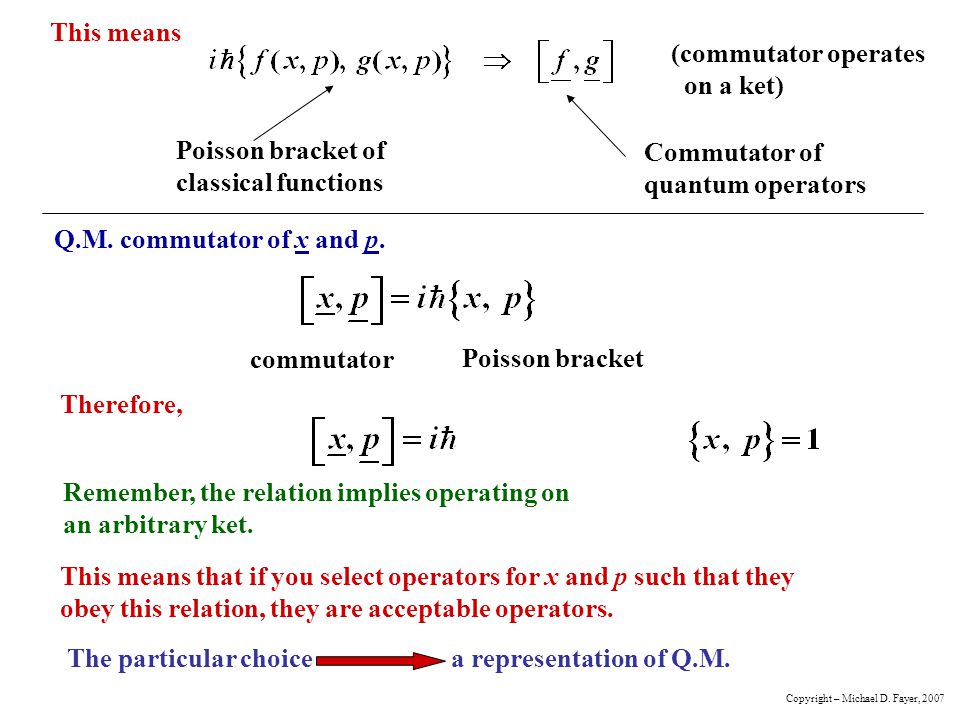
Commutators And The Correspondence Principle Formal Connection Q M Classical Mechanics Correspondence Between Classical Poisson Bracket Of And Q M Commutator Ppt Download

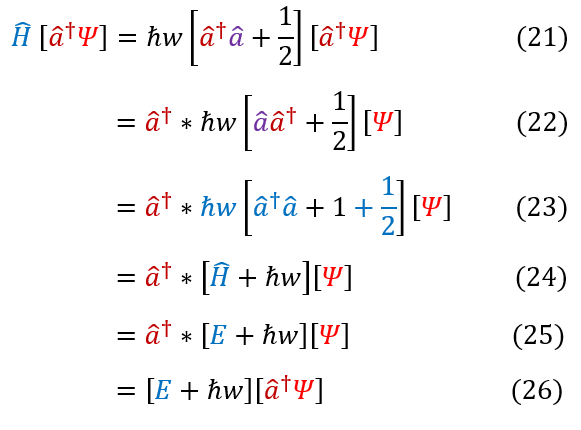
Quantum Harmonic Oscillator Ladder Operators

Www Chem Uzh Ch Dam Jcr Ffffffff 8715 1fca 0000 Pcv Uebungen Pdf

File High Current Copper Brush Commutated Dynamo Jpg Wikimedia Commons

2

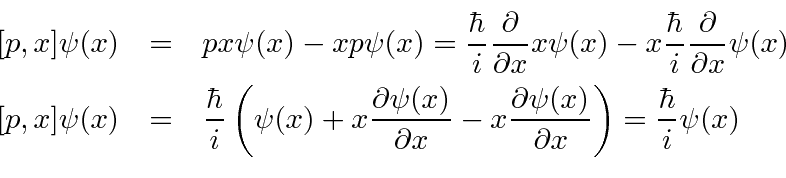
Commutators

3c26qm Pdf By Rdv0044 Issuu

A Little Problem On Lie Brackets Relating It With The Commutator Of Matrices Mathematics Stack Exchange

Phys261 Autumn 14

What Is Commutator X 2 Px 2 Askphysics

Physics Notes

Tbp Berkeley Edu Exams 4435 Download

Www3 Nd Edu Bjanko P Qm1hw3answers Pdf

Projecteuclid Org Download Pdf 1 Euclid Cmp

Solvable Models On Noncommutative Spaces With Minimal Length Uncertai

Topics In Quantum Mechanics Video 18 Momentum And Position Commutator Youtube

22 1 Lecture

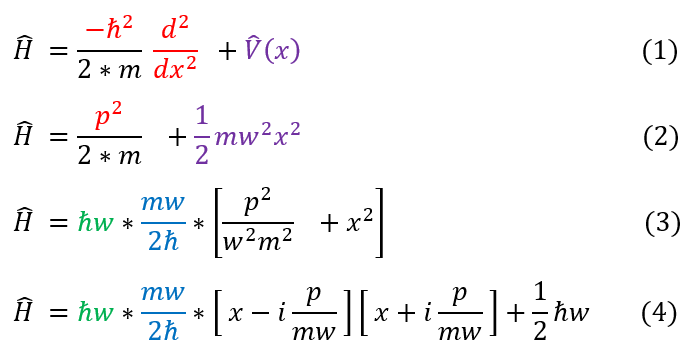
Quantum Harmonic Oscillator Ladder Operators

Commutator Linear Momentum And Position Youtube

Www1 Udel Edu Pchem C444 Splectures supplemental Pdf

Physwww Mcmaster Ca Phys3mm3 Notes Qm3mm3ps6 Pdf

2

Orbital Angular Momentum R Conjugate Momenta P

Incoming Term: p x^2 commutator, commutator x^2 p^3,